지난 글에 이어서 little-\(o\) notation과 little-\(\omega\) notation에 대해 알아봅시다.
little-\(o\) Notation
little-\(o\) 표기는 Big-\(O\) 표기와 유사하게 알고리즘의 점근적 상한을 이용하여 성능을 나타내는 표기법입니다. 하지만 little-\(o\) 표기는 더 엄격한 상한을 나타내는데, 다시말해서 \(f(n)\)이 \(g(n)\)보다 더 엄격하게 작다는 것을 의미합니다. 여기서 엄격하다는 말이 애매하게 들릴 수 있는데, 엄격하다고 해서 little-\(o\) 표기가 성능을 나타내는 데 더 정확한 지표라는 것이 아니고(오히려 반대라고 보면 됩니다), Big-\(O\) 표기는 \(f(n)\)이 \(g(n)\)에 도달할 수 있는 반면에 little-\(o\) 표기는 절대 \(f(n)\)이 \(g(n)\)에 도달할 수 없다는 의미로 엄격하다라는 표현을 사용한 것입니다. 그래서 오히려 최악의 상황에 대해 더욱 정확한 상한을 나타내려면 little-\(o\) 보다는 Big-\(O\)를 사용하기 때문에 little-\(o\) 표기는 자주 사용하지는 않습니다.
그럼, 수학적인 정의를 알아봅시다.
| \(o(g(n)) = \{ f(n)\): 임의의 양의 상수 \(c>0\)에 대해 그리고 모든 \(n\geq n_{0}\)에 대해 \(0\leq f(n)< cg(n)\)인 양의 상수 \(n_{0}\) 가 존재한다.} |
little-\(o\) 표기를 적용한 예시에는 아래와 같은 경우가 있습니다.
| 예1) \(n^2=o(n^3)\): \(n^3\)의 성장률이 \(n^2\)보다 크기 때문에, \(n^3\)의 어떠한 상수배라도 \(n^2\)보다 커지게 되므로 성립합니다. |
| 예2) \(2n^3\neq o(n^3)\): \(n^3\)의 성장률과 \(2n^3\)의 성장률은 상수배를 제외한다면 동일합니다.실제로 \(c=2\)를 선택하면, 둘은 동일하게 되므로 성장률은 비슷하게 됩니다. 이러한 경우때문에 보통은 Big-\(O\) 표기를 사용합니다. |
또한, little-\(o\) 표기의 성립여부를 확인하기 위해서는 다음의 정의도 알아두면 좋습니다.
| \(\lim_{n\to \infty} \frac{f(n)}{g(n)} = 0\) |
little-\(o\) 표기에서는 n이 무한대로 갈수록 함수 f(n)이 g(n)에 비해 보잘 것 없이 작아지기 때문에 위처럼 정의할 수도 있는 것입니다.
little-\(\omega\) Notation
little-\(\omega\) 표기는 little-\(o\)와 반대 개념으로 생각하시면 편합니다. 즉, 알고리즘의 점근적 하한을 나타내는 데 사용합니다. little-\(o\) 표기가 Big-\(O\) 표기보다 엄격한 상한을 나타냈다면, little-\(\omega\)는 Big-\(\Omega\)보다 엄격한 하한을 나타낸다고 할 수 있습니다. 애초에 지난 글에서도 말했듯이 최선의 경우에 대해서 판단하는 상황이 거의 없으므로 사실상 잘 사용하지는 않는 표기법입니다.
그래도 수학적인 정의는 알아둡시다.
| \(\omega(g(n)) = \{ f(n)\): 임의의 양의 상수 \(c>0\)에 대해 그리고 모든 \(n\geq n_{0}\)에 대해 \(0\leq cg(n)<f(n)\)인 양의 상수 \(n_{0}\) 가 존재한다.} |
little-\(\omega\) 표기를 적용한 예시에는 아래와 같은 경우가 있습니다.
| 예1) \(n^3=\omega(n^2)\): \(n^2\)의 성장률이 \(n^3\)보다 작기 때문에, 이 관계는 성립합니다. |
| 예2) \(2n^3\neq \omega(n^3)\): little-\(o\)의 경우와 같이 동일한 성장률을 가지게 되므로 이러한 관계가 나옵니다. |
또한, little-\(\omega\) 표기의 성립여부를 확인하기 위해서는 다음의 정의도 알아두면 좋습니다.
| \(\lim_{n\to \infty} \frac{f(n)}{g(n)} = \infty\) |
little-\(\omega\) 표기에서는 n이 무한대로 갈수록 함수 f(n)이 g(n)과 비교할 수 없이 커지기 때문에 위처럼 정의할 수도 있는 것입니다.
그럼 지금까지 배운 5가지의 점근적 표기법과 관련된 여러 성질들을 알아봅시다.
1. Transitivity
| 1) \(f(n)=\Theta(g(n))\) and \(g(n)=\Theta(h(n))\) imply \(f(n)=\Theta(h(n))\) 2) \(f(n)=O(g(n))\) and \(g(n)=O(h(n))\) imply \(f(n)=O(h(n))\) 3) \(f(n)=\Omega(g(n))\) and \(g(n)=\Omega(h(n))\) imply \(f(n)=\Omega(h(n))\) 4) \(f(n)=o(g(n))\) and \(g(n)=o(h(n))\) imply \(f(n)=o(h(n))\) 5) \(f(n)=\omega(g(n))\) and \(g(n)=\omega(h(n))\) imply \(f(n)=\omega(h(n))\) |
* 'p imply q' 는 'p는 q를 내포하고 있다. p라는 것은 q라고 하는 것과 같다.' 의 느낌으로 이해하면 됩니다.
2. Reflexivity
| 1) \(f(n)=\Theta(f(n))\) 2) \(f(n)=O(f(n))\) 3) \(f(n)=\Omega(f(n))\) |
3. Symmetry
| \(f(n))=\Theta(g(n))\) if and only if \(g(n)=\Theta(f(n))\) |
4. Transpose Symmetry
| 1) \(f(n)=O(g(n))\) if and only if \(g(n)=\Omega(f(n))\) 2) \(f(n)=o(g(n))\) if and only if \(g(n)=\omega(f(n))\) |
그리고 지금까지의 점근적 표기법들의 개념을 이해했다면, 아래와 같이 실수들을 비교하는 느낌으로 외워두면 좀 더 편리할 수 있습니다.
| \(f(n)=\Theta(g(n))\) is like \(a=b\) \(f(n)=O(g(n))\) is like \(a\leq b\) \(f(n)=\Omega(g(n))\) is like \(a\geq b\) \(f(n)=o(g(n))\) is like \(a<b\) \(f(n)=\omega(g(n))\) is like \(a>b\) |
자주 보게될 기본적인 형태의 함수들의 growth ratio 비교는 다음과 같습니다.(밑의 함수정도는 직관적으로도 보일겁니다.)
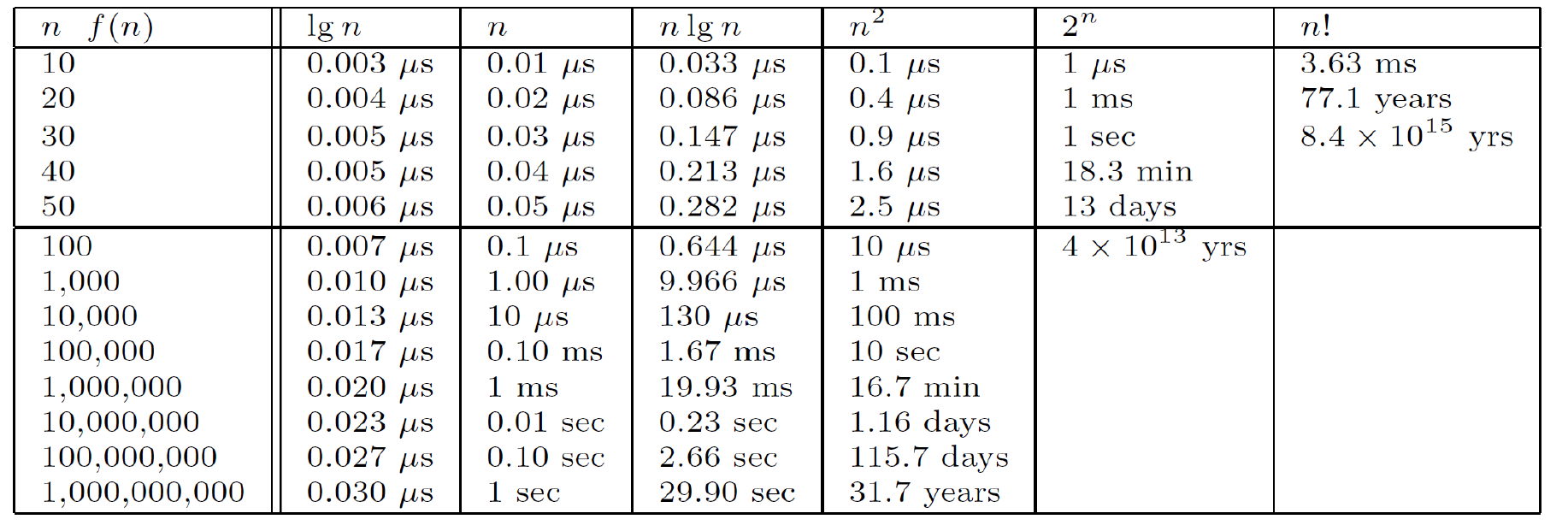
* \(1 << log n << n << nlogn << n^2 << n^3 << 2^n << n!\)
하지만 함수를 언제나 점근적으로 비교할 수 있는 것은 아닙니다. 임의의 두 실수는 항상 비교할 수 있겠지만 예를 들어, 함수 \(n\)과 \(n^{1+\sin n}\)은 후자의 지수 값이 0과 2 사이의 값을 진동하므로 점근적인 비교가 불가능합니다.
또, 위에서 직접 언급은 안 했지만 Big Notation과 little Notation의 차이 중에 하나에는 상수 c의 값이 Big Notation에는 존재하면 되는 것이지만, little Notation은 모든 양의 상수 c에 대한 정의임을 알아두시면 되겠습니다.
ps. 현재 블로그를 막 시작하여 글마다 형식 및 어체의 차이가 있을 수 있는 점 이해해주시면 감사하겠습니다 ㅎㅎ
'Study > 컴퓨터' 카테고리의 다른 글
| 점화식을 푸는 방법 1 :: 치환법 (0) | 2024.05.03 |
|---|---|
| 분할정복과 점화식의 개념 (1) | 2024.05.02 |
| Algorithm Analysis 1 (Big-θ, Big-O, Big-Ω Notation) (0) | 2024.04.28 |


